3.2 正反解多解问题
在求解并联机器人正反解方程的过程中存在方程多解问题:在正解计算中一组实轴坐标对应两组虚轴坐标,其中有一组虚轴坐标位于静平台(平面)上方,可舍去;在反解计算中一组虚轴坐标对应两组实轴坐标,由于本系统具有驱动轴(实轴)单轴手动功能,如果直接舍去反解计算的一组实轴解,会造成手自动切换时系统伺服轴跟随误差出界.产生这种情况的原因是:实轴在单轴手动时可能进入被舍弃的实轴解空间,而实轴单轴手动时系统是不进行反解计算的,因此不会发生报警事件;而在切换到自动状态时反解生效,但实轴解为另一组解,由于理论值与实际值相差很大,造成跟随误差出界报警(如图4 所示).
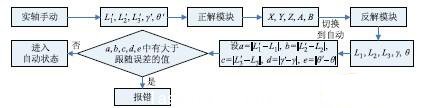
图4 手自动切换过程示意图
为了解决反解多解问题,在反解模块中引入变量来读取实轴实时坐标(),将其与反解计算值() 进行比较,取最接近实轴实时坐标的那组解作为输出,经过处理后驱动实轴运动.为了节省运算时间,此判断过程只在实轴单轴手动切换到自动状态时生效,判断过后一直采用选中的那组解的解析表达式计算实轴坐标,直到下次切换.
3.3 旋转轴“过零”问题
第4 轴(旋转轴)在经过0°点时,会出现突然反转现象:在并联机器人作加工时,在某些位置需要从359.999°运动到0.001°,加工过程只需要旋转轴运动0.002°,而实际情况是旋转轴转动大弧359.998°,产生这种现象的原因是系统将旋转轴当作线性轴来处理,而反解计算只能计算0°到360°的半闭半开区间,旋转轴到360°就会归零.这是加工所不需要的,系统也不可能在一个插补周期内完成一周的转动.
为解决此问题,将第4 轴反解计算值与当前实时坐标相减,然后按下式修正计算值:
 (8)
(8)
式中为修正后的第4轴坐标,为修正前的第4轴坐标计算值,为第4轴的当前实时坐标,| |为向上取整符号.
3.4 加工曲线生成问题
对于5 自由度加工,人工编程有很大难度,而现有的计算机辅助制造(CAM)软件没有针对并联机构的模块.为利用现有的CAM 软件进行加工编程,在位姿正反解模块中加入转换模块,将CAM 中给定的结构和正反解输入输出坐标相互转化.操作者可根据不同的CAM 软件定制不同的转换模块.
以UG的五轴双摆头结构X、Y 、Z、A、B为例说明转换模块的转换过程.首先,为简化转换过程,将第4、第5轴偏置设为0,这样UG在转换时就不考虑刀长,那么UG 输出代码中的X、Y 、Z与并联结构的需求一致,不需要再作转换.我们只需要对刀轴姿态进行转换:设单位刀轴矢量在X 轴的投影为I、在Y轴的投影为J、在Z 轴的投影为K,A为主摆角,B为副摆角,刀具轴在Z轴上,通过数学推导可得出反解模块的刀轴矢量和A、B的关系如下(式中i、j、k依次为矢量I、J、K的模,A、B依次为转角A、B的角度值):
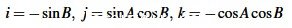 (9)
(9)
同样可得出正解模块的转换关系为:

转载请注明出处。







 相关文章
相关文章
 热门资讯
热门资讯
 精彩导读
精彩导读






























 关注我们
关注我们




