3 位置正反解模块的实现（Realization of the forward and inverse displacement modules）

　　上述功能中，不同于传统数控系统之处在于系统中需要根据机械结构实际的机构模型嵌入特定的位姿正反解模型．因此，建立正确的正反解模型至关重要．

　　3.1 建立正反解几何模型

　　机器人机构简图如图3所示，在本文所述的机构中，将光轴位姿参数（虚轴坐标）换算到驱动坐标位置（实轴坐标）称为反解运算．

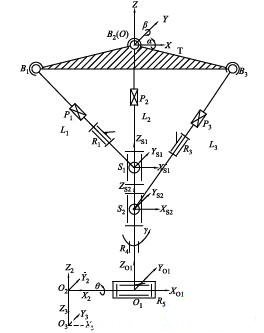
图3 机器人机构简图

　　设定L2分支中绕X 轴旋转虎克铰的旋转角度为α，绕Y轴旋转虎克铰的旋转角度为β，3个分支的杆长分别为L1、L2、L3，串联关节回转转动副和俯仰转动副的转角分别为γ和θ ，则由位姿坐标变换可得到：

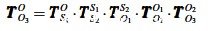(1)

　　已知机器人末端执行器相对于固定参考坐标系O-XYZ 的位姿矩阵：

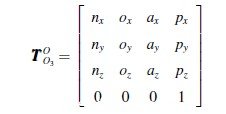(2)

　　求解此矩阵方程可得α、β 、γ 、θ 、．

　　根据求解得到的α、β 和L2，将T_s2^O 和T_O1^O求解出来．得到S2和O1在固定参考坐标系O-XYZ 中的坐标，则得到下式：

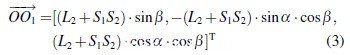
　　在固定平台OB1B3中，OB1B3 为已知三角形，则很容易得到其他两杆长度为：

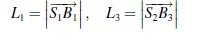(4)

　　正解过程与反解过程正好相反：已知机器人的关节变量L1、L2、L3和γ 、θ ，求解机器人末端位姿矩阵．

　　根据关节变量L1、L2和L3 ，以及B1、O、B3 点坐标，列距离方程可以求解到L2分支绕X 轴和绕Y轴的旋转角度α和β ．其求解方程如下：

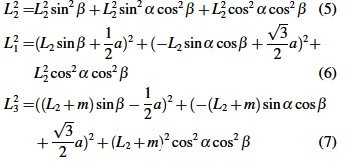
　　根据得到的α和β ，将已知的L2、γ 、θ 代入到位姿变化矩阵，即可将机器人的末端位姿矩阵求解出来，完成运动学正解．